Equivariant Neural Networks
Contents
10. Equivariant Neural Networks#
The previous chapter Input Data & Equivariances discussed data transformation and network architecture decisions that can be made to make a neural network equivariant with respect to translation, rotation, and permutations. However, those ideas limit the expressibility of our networks and are constructed ad-hoc. Now we will take a more systematic approach to defining equivariances and prove that there is only one layer type that can preserve a given equivariance. The result of this section will be layers that can be equivariant with respect to any transform, even for more esoteric cases like points on a sphere or mirror operations. To achieve this, we will need tools from group theory, representation theory, harmonic analysis, and deep learning. Equivariant neural networks are part of a broader topic of geometric deep learning, which is learning with data that has some underlying geometric relationships. Geometric deep learning is thus a broad-topic and includes the “5Gs”: grids, groups, graphs, geodesics, and gauges. However, you’ll see papers with that nomenclature concentrated on point clouds (gauges), whereas graph learning and grids are usually called graph neural networks and convolutions neural networks respectively.
Audience & Objectives
This chapter builds on Input Data & Equivariances and a strong background in math. Although not required, a background on Hilbert spaces, group theory, representation theory, Fourier series, and Lie algebra will help. After completing this chapter, you should be able to
Derive and understand the mathematical foundations of equivariant neural networks
Reason about equivariances of neural networks
Know common symmetry groups
Implement G-equivariant neural network layers
Understand the shape, purpose, and derivation of irreducible function representations
Know how weight-constraints can be used as an alternative
Danger
This chapter teaches how to add equivariance for point clouds, but not permutations. To work with multiple molecules of different size/shape, we need to combine ideas from this chapter with permutation equivariance from the Graph Neural Networks chapter. That combination is explored in Modern Molecular NNs. If you’re always working with atoms/points in the same order, you can ignore permutation equivariance.
10.1. Do you need equivariance?#
Before we get too far, let me first try to talk you out of equivariant networks. The math required is advanced, especially because the theory of these is still in flux. There are five papers in the last few years that propose a general theory for equivariant networks and they each take a slightly different approach [FSIW20, CGW19, KT18, LW20, FWW21]. It is also easy to make mistakes in implementations due to the complexity of the methods. You must also do some of the implementation details yourself, because general efficient implementations of groups is still not solved (although we are getting close now for specifically SE(3)). You will also find that equivariant networks are not in general state of the art on point clouds – although that is starting to change with recent benchmarks set in point cloud segmentation [WAR20], molecular force field prediction [BSS+21], molecular energy predictions [KGrossGunnemann20], and 3D molecular structure generation [SHF+21].
Alternatives to equivariant networks are to just invariant features as discussed in Input Data & Equivariances. Another approach is training and testing augmentation. Both are powerful methods for many domains and are easy to implement [SK19]. You can find details in the Input Data & Equivariances chapter. However, augmentation does not work for locally compact symmetry groups (e.g., SO(3)) — so you cannot use them for rotationally equivariant data. You can do data transformations like discussed in Input Data & Equivariances to avoid equivariance and only work with invariance.
So why would you study this chapter? I think these ideas are important and incorporating the equivariant layers into other network architectures can dramatically reduce parameter numbers and increase training efficiency.
10.2. Running This Notebook#
Click the above to launch this page as an interactive Google Colab. See details below on installing packages.
Tip
To install packages, execute this code in a new cell.
!pip install dmol-book
If you find install problems, you can get the latest working versions of packages used in this book here
10.2.1. Outline#
We have to lay some mathematical foundations before we can grasp the equations and details of equivariant networks. We’ll start with a brief overview of group theory so we can define the principle of equivariance generally. Then we’ll show how any equivariance can be enforced in a neural network via a generalization of convolutions. Then we’ll visit representation theory to see how to encode groups into matrices. Then we’ll see how these convolutions can be more easily represented using the generalization of Fourier transforms. Finally, we’ll examine some implementations. Throughout this chapter we’ll see three examples that capture some of the different settings.
10.3. Group Theory#
A modern treatment of group theory can be found in [Zee16]. You can watch a short fun primer video on group theory from 3Blue1Brown here.
A group is a general object in mathematics. A group is a set of elements that can be combined in a binary operation whose output is another member of the group. The most common example are the integers. If you combine two integers in a binary operation, the output is another integer. Of course, it depends on the operation (
Group Definition
A group
Closure The output of the binary operation is always a member of the group
Associativity
Identity There is a single identity element
Inverse There exists exactly one inverse element
This is quite a bit of nice structure. We always have an inverse available. Applying the binary operations never accidentally leaves our group. One important property that is missing from this list is commutativity. In general, a group is not commutative so that
The point of introducing the groups is so that they can transform elements of our space. This is done through a group action
So a group action takes in two arguments (binary): a group element and a point in a space
Let’s introduce our three example groups that we’ll refer to throughout this chapter.
10.3.1. ⬡ Finite Group
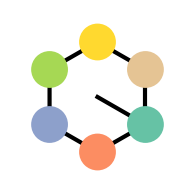
The first group is about rotations of a hexagon 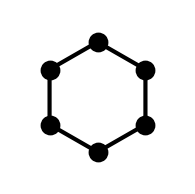 . Our basic group member will be rotating the hexagon enough to shift all the vertices:
. Our basic group member will be rotating the hexagon enough to shift all the vertices: 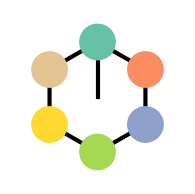
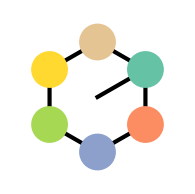 . Notice I’ve colored the vertices and added a line so we can easily distinguish the orientation of the hexagon. Remember the hexagon, its colors, and if it is actually symmetric have nothing to do with the group. The group elements are transformations we apply to the hexagon.
. Notice I’ve colored the vertices and added a line so we can easily distinguish the orientation of the hexagon. Remember the hexagon, its colors, and if it is actually symmetric have nothing to do with the group. The group elements are transformations we apply to the hexagon.
One group action for this example can use modular arithmetic. If we represent a point in our space as
Our group must contain our rotation transformation 

 gives a new group element
gives a new group element
Is this closed? Consider rotating twice and then five times 

 You can see that this is the same as
You can see that this is the same as
In general, we can write out the group as a multiplication table that conveys all group elements and defines the output of all binary outputs:
You can also see that the group is abelian (commutative). For example,
This kind of table is called a Cayley table. Although it doesn’t matter for this example, we’ll see later that the order of look-up matters. Specifically if our group is non-abelian. The row factor comes first and the column factor second. So
This group of rotations is an example of a cyclic group and is isomorphic (same transformations, but operates on different objects) to integers modulo 6. Meaning, you could view rotation
10.3.2. ▩ p4m#
The second group contains translation, 90° rotations, and horizontal/vertical mirroring. We’re now operating on real numbers  ,
,  ,
,  ,
,  What about mirroring on horizontal/vertical? Mirroring along the horizontal axis:
What about mirroring on horizontal/vertical? Mirroring along the horizontal axis: 
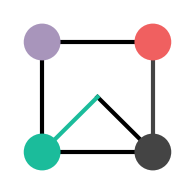 is actually the same as rotating twice and then mirroring along the vertical. In fact, you only need to have mirroring along one axis. We’ll choose the vertical axis by convention and denote that as
is actually the same as rotating twice and then mirroring along the vertical. In fact, you only need to have mirroring along one axis. We’ll choose the vertical axis by convention and denote that as
We can build the group action piece by piece. The group action for rotation can be represented as a 2D rotation matrix acting a point
where
These two group actions can be ordered to correctly represent rotation then mirroring or vice-versa.
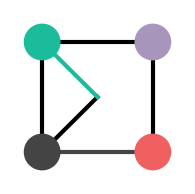
Now is this closed with the group elements  ,
,  ,
,  ,
,  ,
,  ? No. Consider
? No. Consider 

 which is not an element. To close the group, we need
which is not an element. To close the group, we need
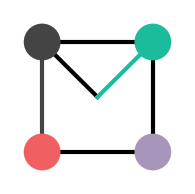
This is a Cayley table. Remember The row factor comes first and the column factor second. So
As you can see from the Cayley table, the group is closed. Remember, elements like 

 , so
, so 

 , which is the group element
, which is the group element
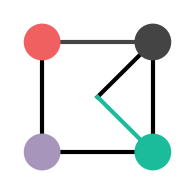
We can also read the inverses off the table. For example, the inverse of
Now consider the translation group elements. For simplicity, let’s only consider integer translations. We can label them as
What about when we combine with our other elements from the
Combing these two groups, the translation and
Below, is an optional section that formalizes the idea of combining these two groups into one larger group.
Normal Subgroup
A normal subgroup is a group of elements
This does not mean
Semidirect Product
Given a normal subgroup of
where
We are technically doing an outer semidirect product: combining them under the assumption that both
One consequence of the semidirect product is that if you have a group element
so
To show what effect the semidirect product has in p4m, we can clean-up our example above about
where
Thus we’ve proved that translating by
10.3.3. ⚽ SO(3) Group#
SO(3) is the group for analyzing 3D point clouds like trajectories or crystal structures (with no other symmetries). SO(3) is the group of all rotations about the origin in 3D. The group is non-abelian because rotations in 3D are not commutative. The group order is infinite, because you can rotate in this group by any angle (or sets of angles). If you are interested in allowing translations, you can use SE(3) which is the semidirect product of SO(3) and the translation group (like p4m), which is a normal subgroup.
The SO(3) name is a bit strange. SO stands for “special orthogonal” which are two properties of square matrices. In this case, the matrices are
One detail is that since we’re rotating (no scale or translation) the distance to origin will not change. We cannot move the radius. The group action is the product of 3 3D rotation matrices (using Euler angles)
10.3.4. Groups on Spaces#
We’ve defined transforms and their relationships to one another via group theory. Now we need to actually connect the transforms to a space. It is helpful to think about the space as Euclidean with a concept of distance and coordinates, but we’ll see that this is not required. Our space could be vertices on a graph or integers or classes. There are some requirements though. The first is that our space must be homogeneous (for the purposes of this chapter). Homogeneous means that from any point
The requirement of space being homogeneous is fairly strict. It means we cannot work with
This may seem like a ton of work. We could have just started with
10.4. Equivariance Definition#
You should be thinking now about how we can define equivariance using our new groups. That’s where we’re headed. We need to do a bit of work now to “lift” neural networks and our features into the framework we’re building. First, in Input Data & Equivariances we defined our features as being composed of tuples
We have promoted our data into a function and now a neural network can no longer be just function since its input is a function. Our neural network will be also promoted to a linear map, which has an input of a function and an output of a function. Formally, our neural network is now
The last piece of equivariance is to promote our group elements, which transform points, to work on functions.
G-Function Transform Definition
An element
This definition takes a moment to think about. Consider a translation of an image. You want to move an image to the left by 10 pixels, so
Now we have all the pieces to define an equivariant neural network:
Equivariant Neural Network Definition
Given a group
where
The definition means that we get the same output if we transform the input function to the neural network or transform the output (in the equivariant case). In a specific example, if we rotate the input by 90 degrees, that’s the same result as rotating the output by 90 degrees. Take a moment to ensure that matches your idea of what equivariance means. After all this math, we’ve generalized equivariance to arbitrary spaces and groups.
What the two input and output spaces? It’s easiest to think about them as the same space for equivariant neural networks. For an invariant, the output space is typically a scalar. Another example for an invariant one could be aligning a molecular structure to a reference. The neural network should align to the same reference regardless of how the input is transformed.
10.5. G-Equivariant Convolution Layers#
Recall that a neural network is made-up of a linear part (e.g.,
G-Equivariant Convolution Theorem
A neural network layer (linear map)
where
where
As you can see from the theorem, we must introduce more new concepts. The first important detail is that all our functions are over our group elements, not our space. This should seem strange. We will easily fix this because there is a way to assign one group element to each point in the space. The second detail is the
There are some interesting notes about this definition. The first is that everything is scalar valued. The weights, which may be called a convolution filter, are coming out of a scalar valued function
Warning
To actually learn, you need to put in a nonlinearity after the convolution. A simple (and often used) case is to just use a standard non-linear function like ReLU pointwise (applied to the output
10.6. Converting between Space and Group#
Let’s see how we can convert between functions on the space
After constructing a subgroup
If this sounds strange, wait for an example.
It turns out if our space is homogeneous we can construct our cosets in a special way so that we have exactly one coset for each point in the space
We will not prove that this is a group itself. This defines our subgroup. Here’s the remarkable thing: we will have exactly enough cosets with this stabilizer as there are points in
Now comes the details, how do we match-up points in
How do we find which coset we need? Since the identity
All that discussion and thinking for such a simple equation. One point to note is that you can plug any element
Going the opposite, from a function on the group to the space, is called projecting because it will have a smaller domain. We can use the same process as above. We create the quotient space and then just take the average over a single coset to get a single value for the point
where we’ve used the fact that
10.7. G-Equivariant Convolutions on Finite Groups#
We now have all the tools to build an equivariant network for a finite group. We’ll continue with our example group
import numpy as np
import matplotlib.pyplot as plt
import dmol
from dmol import color_cycle
Let’s start by defining our input function:
# make our colors (nothing to do with the model)
vertex_colors = []
for c in color_cycle:
hex_color = int(c[1:], 16)
r = hex_color // 256**2
hex_color = hex_color - r * 256**2
g = hex_color // 256
hex_color = hex_color - g * 256
b = hex_color
vertex_colors.append((r / 256, g / 256, b / 256))
vertex_colors = np.array(vertex_colors)
def z6_fxn(x):
return vertex_colors[x]
z6_fxn(0)
array([0.265625, 0.265625, 0.265625])
If we assume our group is indexed already by our vertex coordinates
# make weights be 3x3 matrices at each group element
# 3x3 so that we have 3 color channels in and 3 out
weights = np.random.normal(size=(6, 3, 3))
def z6_omega(x):
return weights[x]
z6_omega(3)
array([[-0.18718385, 1.53277921, 1.46935877],
[ 0.15494743, 0.37816252, -0.88778575],
[-1.98079647, -0.34791215, 0.15634897]])
Now we can define our group convolution operator from Equation 8.6. We do need one helper function to get an inverse group element. Remember too that this returns a function
def z6_inv(g):
return (6 - g) % 6
def z6_prod(g1, g2):
return (g1 + g2) % 6
def conv(f, p):
def out(u):
g = np.arange(6)
# einsum is so we can do matrix product for elements of f and g,
# since we have one matrix per color
c = np.sum(np.einsum("ij,ijk->ik", f(z6_prod(u, z6_inv(g))), p(g)), axis=0)
return c
return out
conv(z6_fxn, z6_omega)(0)
array([ 1.5752359 , 3.70837565, -3.68896212])
At this point, we can now verify that the CNN is equivariant by comparing transforming the input function and the output function. We’ll need to define our function transforms as well.
def z6_fxn_trans(g, f):
return lambda h: f(z6_prod(z6_inv(g), h))
z6_fxn(0), z6_fxn_trans(2, z6_fxn)(0)
(array([0.265625, 0.265625, 0.265625]),
array([0.94921875, 0.70703125, 0.3828125 ]))
First we’ll compute
trans_element = 2
trans_input_fxn = z6_fxn_trans(trans_element, z6_fxn)
trans_input_out = conv(trans_input_fxn, z6_omega)
Now we compute
output_fxn = conv(z6_fxn, z6_omega)
trans_output_out = z6_fxn_trans(trans_element, output_fxn)
print("g -> psi[f(g)], g -> psi[Tgf(g)], g-> Tg psi[f(g)]")
for i in range(6):
print(
i,
np.round(conv(z6_fxn, z6_omega)(i), 2),
np.round(trans_input_out(i), 2),
np.round(trans_output_out(i), 2),
)
g -> psi[f(g)], g -> psi[Tgf(g)], g-> Tg psi[f(g)]
0 [ 1.58 3.71 -3.69] [ 4.16 0.82 -2.78] [ 4.16 0.82 -2.78]
1 [ 4.06 2.55 -3.2 ] [ 2.9 2.33 -2.6 ] [ 2.9 2.33 -2.6 ]
2 [ 2.59 2.34 -1.97] [ 1.58 3.71 -3.69] [ 1.58 3.71 -3.69]
3 [ 2.66 2.25 -1.13] [ 4.06 2.55 -3.2 ] [ 4.06 2.55 -3.2 ]
4 [ 4.16 0.82 -2.78] [ 2.59 2.34 -1.97] [ 2.59 2.34 -1.97]
5 [ 2.9 2.33 -2.6 ] [ 2.66 2.25 -1.13] [ 2.66 2.25 -1.13]
We can see that the outputs indeed match and therefore our network is G-equivariant. One last detail is that it would be nice to visualize this, so we can add a nonlinearity to remap our output back to color space. Our colors should be between 0 and 1, so we can use a sigmoid to put the activations back to valid colors. I’ll hide the input since it contains irrelevant code, but here is the visualization of the previous numbers showing the equivariance.
c1 = conv(z6_fxn, z6_omega)
c2 = trans_input_out
c3 = trans_output_out
titles = [
r"$\psi\left[f(g)\right]$",
r"$\psi\left[\mathbb{T}_2f(g)\right]$",
r"$\mathbb{T}_2\psi\left[f(g)\right]$",
]
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def convert_color(r, g, b):
h = int(sigmoid(r) * 256**3 + sigmoid(g) * 256**2 + sigmoid(b) * 256)
return "#{:6X}".format(h)
c1 = [sigmoid(c1(i)) for i in range(6)]
c2 = [sigmoid(c2(i)) for i in range(6)]
c3 = [sigmoid(c3(i)) for i in range(6)]
fig, axs = plt.subplots(1, 3, squeeze=True)
points = np.array(
[
(0, 1),
(0.5 * np.sqrt(3), 0.5),
(0.5 * np.sqrt(3), -0.5),
(0, -1),
(-0.5 * np.sqrt(3), -0.5),
(-0.5 * np.sqrt(3), 0.5),
]
)
for i in range(3):
axs[i].scatter(points[:, 0], points[:, 1], color=[c1, c2, c3][i])
# plt.plot([0, points[0,0]], [0, points[0, 1]], color='black', zorder=0)
axs[i].set_xticks([])
axs[i].set_yticks([])
axs[i].set_xlim(-1.4, 1.4)
axs[i].set_ylim(-1.4, 1.4)
axs[i].set_aspect("equal")
axs[i].set_title(titles[i], fontsize=8)
plt.show()
As you can see, our output looks the same if we apply the rotation either before or after, so our network is G-equivariant.
10.8. G-Equivariant Convolutions with Translation#
How can we treat the p4m group? We cannot directly use the continuous convolution definition because the rotations/mirror subgroup is finite and we cannot use the finite convolution because the translation subgroup is locally compact (infinitely many elements). Instead, we will exploit the structure of the group: it is constructed via a semidirect product so each group element is a pair of elements. Namely we can rewrite Equation 8.6 using the constituent subgroups
Now we must treat the fact that there are an infinite number of elements in
Our goal for the p4m group is image data, so we’ll limit the support of the kernel to only integer translations (like pixels) and limit the distance to 5 units. This simply reduces our sum over the normal subgroup (
Click to show
# From https://gist.github.com/Susensio/61f4fee01150caaac1e10fc5f005eb75
from functools import lru_cache, wraps
def np_cache(*args, **kwargs):
"""LRU cache implementation for functions whose FIRST parameter is a numpy array
>>> array = np.array([[1, 2, 3], [4, 5, 6]])
>>> @np_cache(maxsize=256)
... def multiply(array, factor):
... print("Calculating...")
... return factor*array
>>> multiply(array, 2)
Calculating...
array([[ 2, 4, 6],
[ 8, 10, 12]])
>>> multiply(array, 2)
array([[ 2, 4, 6],
[ 8, 10, 12]])
>>> multiply.cache_info()
CacheInfo(hits=1, misses=1, maxsize=256, currsize=1)
"""
def decorator(function):
@wraps(function)
def wrapper(np_array, *args, **kwargs):
hashable_array = array_to_tuple(np_array)
return cached_wrapper(hashable_array, *args, **kwargs)
@lru_cache(*args, **kwargs)
def cached_wrapper(hashable_array, *args, **kwargs):
array = np.array(hashable_array)
return function(array, *args, **kwargs)
def array_to_tuple(np_array):
"""Iterates recursivelly."""
try:
return tuple(array_to_tuple(_) for _ in np_array)
except TypeError:
return np_array
# copy lru_cache attributes over too
wrapper.cache_info = cached_wrapper.cache_info
wrapper.cache_clear = cached_wrapper.cache_clear
return wrapper
return decorator
# load image and drop alpha channel
W = 32
try:
func_vals = plt.imread("quadimg.png")[..., :3]
except FileNotFoundError as e:
# maybe on google colab
import urllib.request
urllib.request.urlretrieve(
"https://raw.githubusercontent.com/whitead/dmol-book/main/dl/quadimg.png",
"quadimg.png",
)
func_vals = plt.imread("quadimg.png")[..., :3]
# we pad it with zeros to show boundary
func_vals = np.pad(
func_vals, ((1, 1), (1, 1), (0, 0)), mode="constant", constant_values=0.2
)
def pix_func(x):
# clip & squeeze & round to account for transformed values
xclip = np.squeeze(np.clip(np.round(x), -W // 2 - 1, W // 2)).astype(int)
# points are centered, fix that
xclip += [W // 2, W // 2, 0]
# add 1 to account for padding
return func_vals[xclip[..., 0] + 1, xclip[..., 1] + 1]
def plot_func(f, ax=None):
if ax is None:
plt.figure(figsize=(2, 2))
ax = plt.gca()
gridx, gridy = np.meshgrid(
np.arange(-W // 2, W // 2), np.arange(-W // 2, W // 2), indexing="ij"
)
# make it into batched x,y indices and add dummy 1 indices for augmented space
batched_idx = np.vstack(
(gridx.flatten(), gridy.flatten(), np.ones_like(gridx.flatten()))
).T
ax.imshow(f(batched_idx).reshape(W, W, 3), origin="upper")
ax.axis("off")
plot_func(pix_func)
Now let’s define our G-function transform so that we can transform our function with group elements. We’ll apply a
def make_h(rot, mirror):
"""Make h subgroup element"""
m = np.eye(3)
if mirror:
m = np.array([[-1, 0, 0], [0, 1, 0], [0, 0, 1]])
r = np.array(
[[np.cos(rot), -np.sin(rot), 0], [np.sin(rot), np.cos(rot), 0], [0, 0, 1]]
)
return r @ m
def make_n(dx, dy):
"""Make normal subgroup element"""
return np.array([[1, 0, dx], [0, 1, dy], [0, 0, 1]])
def g_func_trans(g, f):
"""compute g-function transform"""
@np_cache(maxsize=W**3)
def fxn(x, g=g, f=f):
ginv = np.linalg.inv(g)
return f(ginv.reshape(1, 3, 3) @ x.reshape(-1, 3, 1))
return fxn
g = make_h(np.pi, 1) @ make_n(12, -8)
tfunc = g_func_trans(g, pix_func)
plot_func(tfunc)
Now we need to create our lifting and projecting maps to go from functions over points to functions over group elements. Remember, our lifting function just takes the translation element and makes that point.
# enumerate stabilizer subgroup (rotation/mirrors)
stabilizer = []
for i in range(4):
for j in range(2):
stabilizer.append(make_h(i * np.pi / 2, j))
def lift(f):
"""lift f into group"""
# create new function from original
# that is f(gx_0)
@np_cache(maxsize=W**3)
def fxn(g, f=f):
return f(g @ np.array([0, 0, 1]))
return fxn
def project(f):
"""create projected function over space"""
@np_cache(maxsize=W**3)
def fxn(x, f=f):
# x may be batched so we have to allow it to be N x 3
x = np.array(x).reshape((-1, 3))
out = np.zeros((x.shape[0], 3))
for i, xi in enumerate(x):
# find coset gH
g = make_n(xi[0], xi[1])
# loop over coset
for h in stabilizer:
ghi = g @ h
out[i] += f(ghi)
out[i] /= len(stabilizer)
return out
return fxn
# try them out
print("lifted", lift(pix_func)(g))
print("projected", project(lift(pix_func))([12, -8, 0]))
lifted [0.93333334 0.7176471 0.43137255]
projected [[0.72941178 0.71764708 0.72156864]]
We now need to create our kernel functions
kernel_width = 5 # must be odd
# make some random values for kernel (untrained)
# kernel is group elements x 3 x 3. The group elements are structured (for simplicity) as a N x 5 x 5
# the 3 x 3 part is because we have 3 color channels coming in and 3 going out.
kernel = np.random.uniform(
-0.5, 0.5, size=(len(stabilizer), kernel_width, kernel_width, 3, 3)
)
def conv(f, p=kernel):
@np_cache(maxsize=W**4)
def fxn(u):
# It is possible to do this without inner for
# loops over convolution (use a standard conv),
# but we do this for simplicity.
result = 0
for hi, h in enumerate(stabilizer):
for nix in range(-kernel_width // 2, kernel_width // 2 + 1):
for niy in range(-kernel_width // 2, kernel_width // 2 + 1):
result += (
f(u @ make_n(-nix, -niy) @ np.linalg.inv(h))
@ kernel[hi, nix + kernel_width // 2, niy + kernel_width // 2]
)
return sigmoid(result)
return fxn
# compute convolution
cout = conv(lift(pix_func))
# try it out an a group element
cout(g)
array([0.08769476, 0.82036708, 0.99128031])
At this point our convolution layer has returned a function over all group elements. We can visualize this by viewing each stabilizer element individually across the normal subgroup. This is like plotting each coset with a choice of representative element.
def plot_coset(h, f, ax):
"""plot a function over group elements on cosets given representative g"""
gridx, gridy = np.meshgrid(
np.arange(-W // 2, W // 2), np.arange(-W // 2, W // 2), indexing="ij"
)
# make it into batched x,y indices and add dummy 1 indices for augmented space
batched_idx = np.vstack(
(gridx.flatten(), gridy.flatten(), np.ones_like(gridx.flatten()))
).T
values = np.zeros((W**2, 3))
for i, bi in enumerate(batched_idx):
values[i] = f(h @ make_n(bi[0], bi[1]))
ax.imshow(values.reshape(W, W, 3), origin="upper")
ax.axis("off")
# try it with mirror
plt.figure(figsize=(2, 2))
plot_coset(make_h(0, 1), lift(pix_func), ax=plt.gca())
Now we will plot our convolution for each possible coset representative. This code is incredibly inefficient because we have so many loops in plotting and the convolution. This is where the np_cache from above helps.
stabilizer_names = ["$e$", "$r$", "$r^2$", "$r^3$", "$s$", "$rs$", "$r^2s$", "$r^3s$"]
fig, axs = plt.subplots(2, 4, figsize=(8, 4))
axs = axs.flatten()
for i, (n, h) in enumerate(zip(stabilizer_names, stabilizer)):
ax = axs[i]
plot_coset(h, cout, ax)
ax.set_title(n)
These convolutions are untrained, so it’s sort of a diffuse random combination of pixels. You can see each piece of the function broken out by stabilizer group element (the rotation/mirroring). We can stack multiple layers of these convolution if we wanted. At the end, we want to get back to our space with the projection. Let us now show our layers are equivariant by applying a G-function transform to input and output.
fig, axs = plt.subplots(1, 3, squeeze=True)
plot_func(project(cout), ax=axs[0])
axs[0].set_title(r"$\psi\left[f(g)\right]$")
# make a transformation for visualization purposes
g = make_h(np.pi, 0) @ make_n(-10, 16)
tfunc = g_func_trans(g, project(cout))
plot_func(tfunc, ax=axs[1])
axs[1].set_title(r"$\mathbb{T}\psi\left[f(g)\right]$")
tcout = project(conv(lift(g_func_trans(g, pix_func))))
plot_func(tcout, ax=axs[2])
axs[2].set_title(r"$\psi\left[\mathbb{T}f(g)\right]$")
plt.show()
This shows that the convolution layer is indeed equivariant. Details not covered here are how to do pooling (if desired) and the choice of nonlinearity. You can find more details on this for the p4m group in Cohen et al. [CW16]. This implementation is also quite slow! Kondor et al. [KT18] show how you can reduce the number of operations by identifying sparsity in the convolutions.
10.9. Group Representation#
p4m was an infinite group but we restricted ourselves to a finite subset. Before we can progress to truly infinite locally compact groups, like SO(3), we need to learn how to systematically represent the group element binary operation. You can find a detailed description of representation theory in Serre [Ser77] and it is covered in Zee [Zee16]. Thus far, we’ve discussed the group actions – how they affect a point. Now we need to describe how to represent them with matrices. This will be a very quick overview of this topic, but representation of groups is a large area with well-established references. There is specifically a great amount of literature about building up these representations, but we’ll try to focus on using them since you generally can look-up the representations for most groups we’ll operate in.
Let us first define a representation on a group:
Linear Representation of a Group
Let
where the term
There are a few things to note about this definition. First, the representation assigns matrices to group elements in such a way that multiplying matrices gives the same representation as getting the representation of the binary operation (
There is a big detail missing from this definition. Does this have anything to do with how the group element affect a point? No. Consider that
Remember the way a group affects a point is a group action, which maps from the direct product of
Let’s now see group representations on the examples above that are both group actions and representations.
10.9.1. Unitary Representations#
One minor detail is that if we have some representation
because
There is a theorem, the Unitarity Theorem, that says we can always choose an
10.9.2. Irreducible representations#
These representations that both describe the group action and how group elements affect on another are typically reducible, meaning if you drop the requirement that they also describe group action they can be simplified. The process of reducing representations is again a topic better explored in other references [Ser77], but here I will sketch out the important ideas. The main idea is that we can form decomposable unitary representation matrices that are composed of smaller block matrices and zero blocks. These smaller blocks,
This block notation is consistent, regardless of
To add some notation, we use direct sums to write the bigger unitary representation:
and we could just stop the direct sum wherever we would like. The number of irreducible representations is finite for finite groups and infinite for locally compact groups. These irreducible representations are like orthonormal basis-functions or basis-vectors from Hilbert spaces. From the Peter-Weyl theorem, they specifically can be transformed to create a complete basis-set for integrable (
Where do we get these integrable functions? Recall we can use lifting to move functions of our space to our group and then these irreducible representations enable us to represent the functions as a (direct) sum of coefficients of the irreducible representations. Remember, each individual irreducible representation is itself a valid representation, but they are not all faithful and so you need some of them to uniquely represent all group elements and all of them to represent arbitrary functions over the group. One final note, these irreducible representations have been essentially mapped out for all groups and thus we look them up in table rather than try to construct them.
Now we can represent scalar valued functions (
The individual
What is unusual about Equation (10.17) is that for non-abelian groups the individual irreps are matrices of increasing size. How then do we get a scalar out of a product of a vector and a matrix? It turns out we can just do an elementwise dot-product (flatten out the matrix). If you go to construct the fragments for SO(3) (we’ll see how in just a moment), you’ll notice that they are non-unique. That is, the right-hand side seems to be “overpowered” in its representation - it seems capable of representing more.
Indeed, the irreps are for representing the group acting on itself. Imagine a function
where now the
10.10. G-Equivariant Convolutions on Compact Groups#
We’d like to revisit now the G-Equivariant convolution layer equation:
to use irreps now. It turns out that the convolutional integral becomes a product of irreps. This is just like how convolutions in Fourier space become products. [KT18]. Our expression simplifies to:
This result says we just multiply the irreducible representations by weights, but do not mix across irreps. The weights become matrices if we start to allow multiple channels (multiple fragments). How we actually can learn if there is no communication between irreps? That’s where the nonlinearity comes in. It is discussed in more depth below, but the most common nonlinearity is to take a tensor product (all irreps times all irreps) and then reduce that by multiplying the larger rank tensor by a special tensor for the group called Clebsch-Gordan coefficients that reduces it equivariantly back down to the direct sum of irreps. This enables mixing between the irreps and is nonlinear.
10.10.1. Irreducible representations on SO(3)#
There is an infinite sequence of possible irreducible representations for the SO(3) group known as the Wigner D-matrices. These are square matrices that have an odd dimension, and so are traditionally written as the sequence
The Wigner D-matrices are a representation of the group elements (rotations), so it has the properties of a representation. Using
We could use the Wigner D-matrices directly (see discussion in [KLT18]). However, when we lift our input function (input points) into the group, each point in our space maps to multiple group elements (the cosets discussed above). Instead of working with such redundant representation, we can work with spherical harmonics that give vectors instead of matrices for a particular choice of irrep index
To be more specific, remember our conversion from an input
So what can we do here? We desire a set of
Spherical harmonics, usually written as
Note in this equation that
Warning
Although we’ll use spherical harmonics, I and many authors may still refer
We do have a choice of
10.10.2. SO(3) Nonlinearity & Mixing#
We’ll continue on using spherical harmonics and will get to a layer like that presented in the Tensor Field Network paper [TSK+18] and Cormorant paper [AHK19]. There are two equations for equivariant nonlinearity in SO(3), and they are sometimes combined. The first nonlinearity is a Clebsch-Gordan tensor product and enables mixing between irreps. The equation is
where
As before,
There is another kind of nonlinearity that is equivariant called gated nonlinearities [WGW+18]. The equation is simple; just compute the magnitude of each of the irrep fragments
The gated nonlinearity is sometimes used instead of Equation (10.21) or as an extra step after it [TSK+18].
At the end of the network, most of the time we simply take the
10.11. SO(3) Equivariant Example#
Let’s implement a non-differentiable version of the equations above for the SO(3) group. To begin, let’s write the code to convert our points into their irreps using real spherical harmonics. Our code is not differentiable, so we won’t be able to train.
import numpy as np
from scipy.special import sph_harm
def cart2irreps(x, L):
"""
input N x 3 points and number of irreps (L)
output L x N x M(l)
"""
# convert to spherical coords and then evaluate
# in spherical harmonics to get irrep values
N = x.shape[0]
r = np.linalg.norm(x, axis=-1)
azimuth = np.arctan2(x[:, 1], x[:, 0])
polar = np.arccos(x[:, 2], r)
f = []
for l in range(L):
fi = []
for m in range(-l, l + 1):
y = sph_harm(m, l, azimuth, polar)
fi.append(y)
fi = np.array(fi)
f.append(fi.T) # transpose so N (particles) is first axes
return f
def print_irreps(f):
for i in range(len(f)):
if len(f[0].shape) == 3:
print(f"irrep {i} ({f[i].shape[-1]} channels)")
else:
print(f"irrep {i} (no channels)")
print(f[i])
points = np.random.rand(2, 3)
L = 3 # number of irreps
f = cart2irreps(points, L)
print_irreps(f)
irrep 0 (no channels)
[[0.28209479+0.j]
[0.28209479+0.j]]
irrep 1 (no channels)
[[ 0.04759512-0.0906715j 0.46664674+0.j -0.04759512-0.0906715j ]
[ 0.14047877-0.23554538j 0.29715416+0.j -0.14047877-0.23554538j]]
irrep 2 (no channels)
[[-0.01927396-0.02793043j 0.10164359-0.193637j 0.54765934+0.j
-0.10164359-0.193637j -0.01927396+0.02793043j]
[-0.11567994-0.21415567j 0.1910389 -0.32032122j 0.0345726 +0.j
-0.1910389 -0.32032122j -0.11567994+0.21415567j]]
We chose to use 3 irreps here and get a fragment vector for each particle at each irrep. This gives a scalar for
Notice that
def rbf(r, c):
mu = np.linspace(0, 1, c)
gamma = 10 / c # just pick gamma to be rmax / c
return np.exp(-gamma * (r - mu[..., None]) ** 2)
def cart2irreps_channels(x, L, C):
"""
input N x 3 points and number of irreps (L)
output L x N x M(l) x C
"""
# convert to spherical coords and then evaluate
# in spherical harmonics to get irrep values
N = x.shape[0]
r = np.linalg.norm(x, axis=-1)
rc = rbf(r, C)
azimuth = np.arctan2(x[:, 1], x[:, 0])
polar = np.arccos(x[:, 2], r)
f = []
for l in range(L):
fi = []
for m in range(-l, l + 1):
y = sph_harm(m, l, azimuth, polar)
fi.append(y)
fi = np.array(fi).T # transpose so N (particles) is first axes
fic = np.einsum(
"ij,ci->ijc", fi, rc
) # outer product (all irreps with all channels)
f.append(fic)
return f
C = 3 # number of channels
f = cart2irreps_channels(points, L, C)
print_irreps(f)
irrep 0 (3 channels)
[[[0.00055928+0.j 0.02310789+0.j 0.18032962+0.j]]
[[0.00268624+0.j 0.05995227+0.j 0.25272152+0.j]]]
irrep 1 (3 channels)
[[[ 9.43618923e-05-1.79764937e-04j 3.89877000e-03-7.42738542e-03j
3.04252708e-02-5.79619247e-02j]
[ 9.25171857e-04+0.00000000e+00j 3.82255187e-02+0.00000000e+00j
2.98304788e-01+0.00000000e+00j]
[-9.43618923e-05-1.79764937e-04j -3.89877000e-03-7.42738542e-03j
-3.04252708e-02-5.79619247e-02j]]
[[ 1.33770537e-03-2.24297469e-03j 2.98552853e-02-5.00593409e-02j
1.25851340e-01-2.11019089e-01j]
[ 2.82964275e-03+0.00000000e+00j 6.31527639e-02+0.00000000e+00j
2.66212828e-01+0.00000000e+00j]
[-1.33770537e-03-2.24297469e-03j -2.98552853e-02-5.00593409e-02j
-1.25851340e-01-2.11019089e-01j]]]
irrep 2 (3 channels)
[[[-3.82124628e-05-5.53747472e-05j -1.57883230e-03-2.28792998e-03j
-1.23209116e-02-1.78545771e-02j]
[ 2.01518158e-04-3.83903906e-04j 8.32616779e-03-1.58618378e-02j
6.49758540e-02-1.23782811e-01j]
[ 1.08578709e-03+0.00000000e+00j 4.48616919e-02+0.00000000e+00j
3.50092241e-01+0.00000000e+00j]
[-2.01518158e-04-3.83903906e-04j -8.32616779e-03-1.58618378e-02j
-6.49758540e-02-1.23782811e-01j]
[-3.82124628e-05+5.53747472e-05j -1.57883230e-03+2.28792998e-03j
-1.23209116e-02+1.78545771e-02j]]
[[-1.10155920e-03-2.03929175e-03j -2.45849084e-02-4.55134876e-02j
-1.03634704e-01-1.91856595e-01j]
[ 1.81916294e-03-3.05025046e-03j 4.06005908e-02-6.80763488e-02j
1.71146874e-01-2.86967604e-01j]
[ 3.29216707e-04+0.00000000e+00j 7.34755118e-03+0.00000000e+00j
3.09727122e-02+0.00000000e+00j]
[-1.81916294e-03-3.05025046e-03j -4.06005908e-02-6.80763488e-02j
-1.71146874e-01-2.86967604e-01j]
[-1.10155920e-03+2.03929175e-03j -2.45849084e-02+4.55134876e-02j
-1.03634704e-01+1.91856595e-01j]]]
Let’s now implement the linear part - Equation (10.20)
def linear(f, W):
for l in range(len(f)):
f[l] = np.einsum("ijk,kl->ijl", f[l], W[l])
return f
def init_weights(cin, cout, L=L):
return np.random.randn(L, cin, cout)
weights = init_weights(C, C)
print("Input shapes", ",".join([str(f[i].shape) for i in range(L)]))
h = linear(f, weights)
print("Output shapes", ",".join([str(h[i].shape) for i in range(L)]))
print_irreps(h)
Input shapes (2, 1, 3),(2, 3, 3),(2, 5, 3)
Output shapes (2, 1, 3),(2, 3, 3),(2, 5, 3)
irrep 0 (3 channels)
[[[-0.14579183+0.j 0.13672409+0.j 0.15786851+0.j]]
[[-0.27630188+0.j 0.15265833+0.j 0.23632184+0.j]]]
irrep 1 (3 channels)
[[[ 0.01979472-0.03771011j 0.01273654-0.02426386j
0.02532457-0.04824479j]
[ 0.19407749+0.j 0.12487552+0.j
0.24829491+0.j ]
[-0.01979472-0.03771011j -0.01273654-0.02426386j
-0.02532457-0.04824479j]]
[[ 0.08276803-0.13877988j 0.03964979-0.06648211j
0.11796382-0.19779383j]
[ 0.17507888+0.j 0.08387104+0.j
0.2495284 +0.j ]
[-0.08276803-0.13877988j -0.03964979-0.06648211j
-0.11796382-0.19779383j]]]
irrep 2 (3 channels)
[[[-0.00474219-0.00687205j -0.00836849-0.01212701j
-0.00118678-0.00171979j]
[ 0.02500855-0.04764275j 0.04413226-0.08407455j
0.00625862-0.01192303j]
[ 0.13474694+0.j 0.23778622+0.j
0.03372165+0.j ]
[-0.02500855-0.04764275j -0.04413226-0.08407455j
-0.00625862-0.01192303j]
[-0.00474219+0.00687205j -0.00836849+0.01212701j
-0.00118678+0.00171979j]]
[[-0.04248787-0.07865684j -0.07325579-0.13561679j
-0.01926609-0.03566688j]
[ 0.07016632-0.11765019j 0.12097781-0.20284747j
0.03181687-0.05334839j]
[ 0.01269811+0.j 0.02189354+0.j
0.00575795+0.j ]
[-0.07016632-0.11765019j -0.12097781-0.20284747j
-0.03181687-0.05334839j]
[-0.04248787+0.07865684j -0.07325579+0.13561679j
-0.01926609+0.03566688j]]]
You can see that we now have multiple channels at each irrep. Our tensors are
Now we’ll implement the Clebsch-Gordan nonlinearity, Equation (10.21). We need to get the Clebsch-Gordan coefficients. These are tabulated for the application of computing angular momentum coupling in quantum systems. We’ll use specifically the package in scipy.
from functools import lru_cache
from scipy.special import sph_harm
from sympy import S
from sympy.physics.quantum.cg import CG as sympy_cg
# to speed-up repeated calls, put a cache around it
@lru_cache(maxsize=10000)
def CG(i, j, k, l, m, n):
# to get a float, we wrap input in symbol (S), call
# doit, and evalf.
r = sympy_cg(S(i), S(j), S(k), S(l), S(m), S(n)).doit().evalf()
return float(r)
CG(1, 0, 1, 0, 0, 0)
-0.5773502691896257
If you would like to see how to compute the coefficients with real spherical harmonics and/or avoid using sympy, you can show the cells below to learn how to compute Clebsch-Gordan coefficients.
Now we’ll implement the Clebsch-Gordan nonlinearity, Equation {eq}cg-nl. We’ll use the coefficients in sympy, but we need to put a minus sign into the Clebsch-Gordan coefficients from Sympy to get them to work with our real-valued spherical harmonics.
# As you can see, the Clebsch-Gordan nonlinearity is a lot!!
# i -> left input irrep index
# j -> left input irrep fragment i index (shifted for use in CG)
# k -> right input irrep index
# l -> right input irrep fragment k index (shifted for use in CG)
# m -> output irrep index
# n -> output irrep fragment m index
# implicit broadcasted indices -> particles (fragment index 0) and channels (fragment index 2)
def cgnl(f):
L = len(f)
output = [np.zeros_like(fi) for fi in f]
for i in range(L):
for j in range(-i, i + 1):
for k in range(L):
for l in range(-k, k + 1):
for m in range(L):
for n in range(-m, m + 1):
output[m][:, n + m] += (
f[i][:, j + i] * f[k][:, l + k] * CG(i, j, k, l, m, n)
)
return output
A small note - sometimes you’ll see the CG layer part not just sum over the products (right-hand side). Instead they will concat along the channel axis into a long vector per irrep index and then mix them with a dense layer.
Now we can make our complete layer! We won’t use a gated nonlinearity here, just the Clebsch-Gordan nonlinearity.
def cg_net(x, W, L, C, num_layers):
f = cart2irreps_channels(x, L, C)
for i in range(num_layers):
f = linear(f, W[i])
f = cgnl(f)
return np.squeeze(f[0])
num_layers = 3
L = 3 # note if you go higher, you need to adjust CG code
channels = 4
weights = (
[init_weights(channels, channels, L)]
+ [init_weights(channels, channels, L) for _ in range(num_layers - 2)]
+ [init_weights(channels, 1, L)]
)
cg_net(points, weights, L, channels, num_layers)
array([0.0006764 -5.55317441e-20j, 0.01278468-6.60074738e-19j])
Now we have our irrep features. How do we get an output? If we’re trying to output a scalar (regression/classification), we would just take the
Let us now check that our network is indeed invariant (we’re outputting a single value per point, so invariant). We’ll make a rotation and check if our output changes.
# random 3x3 matrix
R = np.random.rand(3, 3)
# make it a member of SO(3)
U, _, V = np.linalg.svd(R)
R = np.dot(U, V)
points = np.random.rand(2, 3)
print(points)
[[0.74910061 0.53233607 0.11495215]
[0.39362975 0.37554936 0.56816224]]
print(cg_net(points, weights, L, channels, num_layers))
print(cg_net(points @ R, weights, L, channels, num_layers))
[0.03947039-2.00880578e-18j 0.29290328+1.79370610e-16j]
[0.03947039-2.60616101e-17j 0.29290328-1.47285660e-16j]
As we can see, rotating the input points has no effect on the output! Remember, we we will treat permutation equivariance in future chapters – this network is sensitive to the order of the input coordinates.
10.11.1. Computing the Clebsch-Gordan coefficients#
Just like the fact that there are multiple choices in the irrep (the unitary matrix
Where I’ve not used the vector notation for
Click to show
def cart2irreps_real(x, M):
# convert to spherical coords and then evaluate
# in spherical harmonics to get irrep values
N = x.shape[0]
r = np.linalg.norm(x, axis=-1)
azimuth = np.arctan2(x[:, 1], x[:, 0])
polar = np.arccos(x[:, 2], r)
f = []
for m in range(M):
fi = []
for l in range(-m, m + 1):
# convert to real (Condon-Shortley Phase Convention should be included from scipy?)
if m < 0:
y = sph_harm(l, abs(m), azimuth, polar)
y = np.sqrt(2) * y.imag
elif m > 0:
y = sph_harm(l, m, azimuth, polar)
y = np.sqrt(2) * y.real
else:
y = sph_harm(l, m, azimuth, polar)
fi.append(y.real)
fi = np.array(fi)
f.append(fi.T)
return f
@lru_cache(maxsize=1000)
def _compute_CG(l1, m1, l2, m2, N=5000):
l_max = 3
num_coefs = sum([(2 * j + 1) for j in range(l_max + 1)])
# make points
points = np.random.uniform(-1, 1, size=(N, 3))
# make them be on unit sphere
points /= np.linalg.norm(points, axis=-1)[:, np.newaxis]
# compute their irreps
# l1 + l1 -> go from negative number to start from zero.
all_irreps = cart2irreps_real(points, l_max + 1)
D1 = all_irreps[l1][:, l1 + m1]
D2 = all_irreps[l2][:, l2 + m2]
target = D1 * D2
A = np.zeros((N, num_coefs))
for i in range(N):
ds = [all_irreps[l][i, :] for l in range(0, l_max + 1)]
Ds = np.concatenate(ds)
A[i, :] = Ds
flat_coeffs = np.linalg.pinv(A, rcond=10**-5) @ target
error = np.mean((A @ flat_coeffs - target) ** 2)
assert error < 0.1, "CG error seems high at" + str(error)
# unflatten it
coeffs = []
j = 0
for i in range(l_max + 1):
coeffs.append(flat_coeffs[j : j + 2 * i + 1])
return coeffs
@lru_cache(maxsize=10000)
def CG2(l1, m1, l2, m2, L, M):
cg = _compute_CG(l1, m1, l2, m2)
return cg[L][M + L]
CG2(2, 0, 2, 0, 0, 0)
0.44724838464333005
10.11.2. E3NN Tutorial#
You can find an example using the modern e3nn package to predict trajectory frames in Equivariant Neural Network for Predicting Trajectories.
10.12. Equivariant Neural Networks with Constraints#
You do not need to use irreducible representations. It is currently in 2022 the dominant paradigm due to its good accuracy. There are approaches like just staying in Cartesian coordinates and using Clifford Algebra instead of Clebsch-Gordon products to mix scalars and vectors [Spe21]. Another alternative is to work in the defining/faithful representation and put equivariant constraints on your network weights. Let’s see an example of this approach via the library released by the authors called Equivariant MLP (emlp)[FWW21]
We’ll create an SO(3) equivariant neural network and check that it is equivariant to rotations. We begin by defining our group and its representation. I’ll show a few elements too, to demonstrate that this is the faithful representation and not the irreducible.
from emlp.groups import SO, S
import emlp.reps as reps
import emlp
import haiku as hk
import emlp.nn.haiku as ehk
import jax.numpy as jnp
so3_rep = reps.V(SO(3))
# grab a random group element
sampled_g = SO(3).sample()
dense_rep = so3_rep.rho(sampled_g)
# check its a member of SO(3)
# g @ g.T = I
print(dense_rep @ dense_rep.T)
No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
[[ 9.9999994e-01 -6.2375683e-08 -3.7966075e-08]
[-6.2375683e-08 9.9999994e-01 -3.8163165e-08]
[-3.7966075e-08 -3.8163165e-08 1.0000001e+00]]
Now we’ll apply our group element to a point to see it rotate the point. The norm should be unchanged, because it’s a rotation.
point = np.array([0, 0, 1])
print("new point", dense_rep @ point.T)
print("norm", np.sqrt(np.sum((dense_rep @ point) ** 2)))
new point [0.327511 0.92194474 0.20677114]
norm 0.99999994
Now let’s assume our input function consists of 5 points (e.g., methanol molecule) defined by features (e.g., 1D element embedding) and positions. We’ll create that as a direct sum of 5 scalars and 5 vectors. Our output will be a vector (e.g., dipole). Equivariance here will then mean that if rotate the input points, our output vector should undergo the same rotation.
input_rep = 5 * so3_rep**0 + 5 * so3_rep**1
print("input rep", input_rep)
print("output rep", so3_rep)
input_point = np.random.randn(5 + 5 * 3)
print("input features", input_point[:5])
print("input positions\n", input_point[5:].reshape(5, 3))
input rep 5V⁰+5V
output rep V
input features [-0.85729602 -1.11020333 1.01666215 1.50028049 2.53586486]
input positions
[[ 1.88610779 0.43249119 -0.20274311]
[ 0.15031153 -1.05175462 0.99108185]
[ 0.01070065 1.33751242 -0.31244968]
[-0.08570713 -1.97083479 -0.69204595]
[-2.07402069 0.09111016 -0.36870261]]
model = emlp.nn.EMLP(input_rep, so3_rep, group=SO(3), num_layers=1)
output_point = model(input_point)
print("output", output_point)
output [ 0.0178488 -0.01094992 -0.00513285]
Now we’ll transform the input points according to a random element in the group. We could convert the input into the five spatial vectors and apply the group element to them individually and put them back together. However, emlp has a convenience function for exactly that. We can change our group element to the input representation.
trans_input_point = input_rep.rho_dense(sampled_g) @ input_point
print("transformed input features", trans_input_point[:5])
print("transformed input positions\n", trans_input_point[5:].reshape(5, 3))
transformed input features [-0.85729605 -1.1102034 1.0166621 1.5002805 2.5358648 ]
transformed input positions
[[-0.28291723 0.30680364 -1.9003646 ]
[ 1.3278114 0.5826005 0.09229225]
[-1.3578111 0.17007749 -0.11874735]
[ 1.6162695 -1.3259373 0.00507326]
[-0.41505656 -0.6895579 1.9488567 ]]
Now we compare running the transformed input through the model against applying the group element to the output from the untransformed input.
model(trans_input_point), sampled_g @ output_point
(Array([ 0.01040221, -0.00519046, -0.01815708], dtype=float32),
Array([ 0.0104022 , -0.00519046, -0.01815709], dtype=float32))
Indeed they are equivalent – meaning this model is equivariant. The constraint approach is quite simple to use and can handle arbitrary groups. However, it may not be efficient when working with many input points (like a protein) and it may make sense to use an implementation specific to E(3) or SO(3).
10.12.1. How the constraints work#
How does this magic happen? Rather than explicitly setting constraints on the dense layer weights, emlp always first projects the network weights into an equivariant subspace. This means that the cost of equivariance is paid when constructing the model when this projection matrix is found but not later during training and inference. The equivariant subspace is the space of allowed weights that respect the equivariance. Let’s see what this looks like.
Recall that a dense layer has the equation:
where
Let’s start by making these projectors.
Pw = (input_rep >> so3_rep).equivariant_projector()
Pb = (so3_rep).equivariant_projector()
print("Pw shape is", Pw.shape, "Pb shape is", Pb.shape)
Pw shape is (60, 60) Pb shape is (3, 3)
Note that they are square because they should leave the underlying dimension of
Now let’s show how these projectors can convert an arbitrary weight matrix into one that is equivariant.
W = np.random.randn(3, 5 + 5 * 3)
b = np.random.randn(3)
print(
"W is not alone equivariant",
W @ trans_input_point.flatten(),
"!=",
sampled_g @ W @ input_point,
)
W is not alone equivariant [-6.049798 6.7904463 -5.1393642] != [-0.69973874 -2.128122 -0.7788652 ]
Proj_W = (Pw @ W.flatten()).reshape(W.shape)
print(
"Projected W is equivariant",
Proj_W @ trans_input_point.flatten(),
"==",
sampled_g @ Proj_W @ input_point,
)
Projected W is equivariant [ 0.92439556 2.389505 -2.6037421 ] == [ 0.9243953 2.389505 -2.603743 ]
You may be wondering how much the projection affects
plt.title("Random W")
plt.imshow(W)
plt.show()
plt.title("Projected W")
plt.imshow(Proj_W)
plt.show()
It appears that there are only a few unique values in emlp can be more expensive. We’re training 180 values but we could have just used a few. Similarly, the projected bias is zero for our system.
Pb @ b
Array([0., 0., 0.], dtype=float32)
10.12.2. Including Permutation Groups#
In real molecules, we also need to have permutation equivariance with respect to the atom ordering and bond ordering – which is not true of our above example about computing dipole moment. emlp also supports permutation groups, which are usually written as emlp to treat the permutation equivariance. We’ll work on that in the next chapter!
10.13. Chapter Summary#
Equivariant neural networks guarantee equivariance by construction for arbitrary groups, which removes the need to align trajectories, work in special coordinate systems, or use pairwise distances.
Equivariance can be achieved by parameter sharing or testing/training data augmentation, but here we focused on equivariant layers that can be composed into a neural network.
Equivariance requires definition of a group and homogeneous space. We must view our input data as functions and our models as operators that transform functions.
Finite groups can be treated with G-equivariant layers that have an additional sum across a specific subgroup.
Infinite groups like SO(3) can be made finite by working with a direct sum (list of vectors) of the irreducible representations. This requires converting the input data though to the irreducible representation and there are complexities in nonlinearities and implementations typically are sophisticated.
Constraint-based equivariant layers are flexible, general, and quick to implement but may not scale well with respect to size of input group or number of points.
Recent work has also shown you can put irreducible representation direct sums into the edges of graph neural networks, gaining input size independence, permutation invariance, and spatial equivariance in one model.
10.14. Exercises#
Does the picture
 represent a point in the space or function in the space? Justify your answer
represent a point in the space or function in the space? Justify your answerIn the
Is the defining representation always faithful?
Let’s redefine our space for p4m to have
Explain how the code example above deals with channels and compare with your answer to 4.
The output from a G-equivariant neural network is a scalar valued function. Would taking the value at a specific point of the function be equivariant, invariant, or neither? What about a definite integral over the function?
You can represent permutations as a group. For example, given a sequence a,b,c you can represent swapping position 1 and 2 as an element from a group. Write the Caley table for such a group. What is the space for this example and what needs to be true for it to be homogeneous.
In the G-equivariant neural network layer definition, the output space can be different. Does it have to be homogeneous for the definition to hold? Why or why not? What if the input space is points and the output space is a multi-class probability vector – can you have equivariance? Why or why not?
Could we make a scale equivariant neural network? A scale being some constant
If we add a new dimension to the space that, by construction, is unaffected by the group action then is the space still homogeneous? If so, can we change our space, group, or action to make the space homogeneous?
10.15. Relevant Videos#
10.15.1. Intro to Geometric Deep Learning#
10.15.2. Equivariant Networks#
10.15.3. Equivariant Network Tutorial#
10.16. Cited References#
- TSK+18(1,2)
Nathaniel Thomas, Tess Smidt, Steven Kearnes, Lusann Yang, Li Li, Kai Kohlhoff, and Patrick Riley. Tensor field networks: rotation-and translation-equivariant neural networks for 3d point clouds. arXiv preprint arXiv:1802.08219, 2018.
- WGW+18(1,2)
Maurice Weiler, Mario Geiger, Max Welling, Wouter Boomsma, and Taco S Cohen. 3d steerable cnns: learning rotationally equivariant features in volumetric data. In Advances in Neural Information Processing Systems, 10381–10392. 2018.
- FSIW20(1,2)
Marc Finzi, Samuel Stanton, Pavel Izmailov, and Andrew Gordon Wilson. Generalizing convolutional neural networks for equivariance to lie groups on arbitrary continuous data. arXiv preprint arXiv:2002.12880, 2020.
- CGW19
Taco S Cohen, Mario Geiger, and Maurice Weiler. A general theory of equivariant cnns on homogeneous spaces. Advances in neural information processing systems, 32:9145–9156, 2019.
- KT18(1,2,3,4)
Risi Kondor and Shubhendu Trivedi. On the generalization of equivariance and convolution in neural networks to the action of compact groups. In International Conference on Machine Learning, 2747–2755. 2018.
- LW20
Leon Lang and Maurice Weiler. A wigner-eckart theorem for group equivariant convolution kernels. arXiv preprint arXiv:2010.10952, 2020.
- FWW21(1,2)
Marc Finzi, Max Welling, and Andrew Gordon Wilson. A practical method for constructing equivariant multilayer perceptrons for arbitrary matrix groups. Arxiv, 2021.
- WAR20
Renhao Wang, Marjan Albooyeh, and Siamak Ravanbakhsh. Equivariant maps for hierarchical structures. arXiv preprint arXiv:2006.03627, 2020.
- BSS+21
Simon Batzner, Tess E. Smidt, Lixin Sun, Jonathan P. Mailoa, Mordechai Kornbluth, Nicola Molinari, and Boris Kozinsky. Se(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. arXiv preprint arXiv:2101.03164, 2021.
- KGrossGunnemann20
Johannes Klicpera, Janek Groß, and Stephan Günnemann. Directional message passing for molecular graphs. arXiv preprint arXiv:2003.03123, 2020.
- SHF+21
Victor Garcia Satorras, Emiel Hoogeboom, Fabian B. Fuchs, Ingmar Posner, and Max Welling. E(n) equivariant normalizing flows for molecule generation in 3d. arXiv preprint arXiv:2105.09016, 2021.
- SK19
Connor Shorten and Taghi M Khoshgoftaar. A survey on image data augmentation for deep learning. Journal of big data, 6(1):1–48, 2019.
- Zee16(1,2)
Anthony Zee. Group theory in a nutshell for physicists. Princeton University Press, 2016.
- RBTH20
David W Romero, Erik J Bekkers, Jakub M Tomczak, and Mark Hoogendoorn. Attentive group equivariant convolutional networks. arXiv, pages arXiv–2002, 2020.
- CW16(1,2)
Taco Cohen and Max Welling. Group equivariant convolutional networks. In International conference on machine learning, 2990–2999. 2016.
- Ser77(1,2)
Jean-Pierre Serre. Linear representations of finite groups. Volume 42. Springer, 1977.
- KLT18(1,2)
Risi Kondor, Zhen Lin, and Shubhendu Trivedi. Clebsch-gordan nets: a fully fourier space spherical convolutional neural network. arXiv preprint arXiv:1806.09231, 2018.
- AHK19
Brandon Anderson, Truong Son Hy, and Risi Kondor. Cormorant: covariant molecular neural networks. Advances in neural information processing systems, 2019.
- Spe21
Matthew Spellings. Geometric algebra attention networks for small point clouds. arXiv preprint arXiv:2110.02393, 2021.

